Deep learning is typically applied to Euclidean data. Datatypes in the 1- and 2-dimensional domains are included in this. However, we don’t live in a 1D or 2D universe. Everything we can see is three-dimensional, thus our data needs to show this. It’s high time machine learning caught up to us. Euclidean data includes text, images, audio files, and many more types.
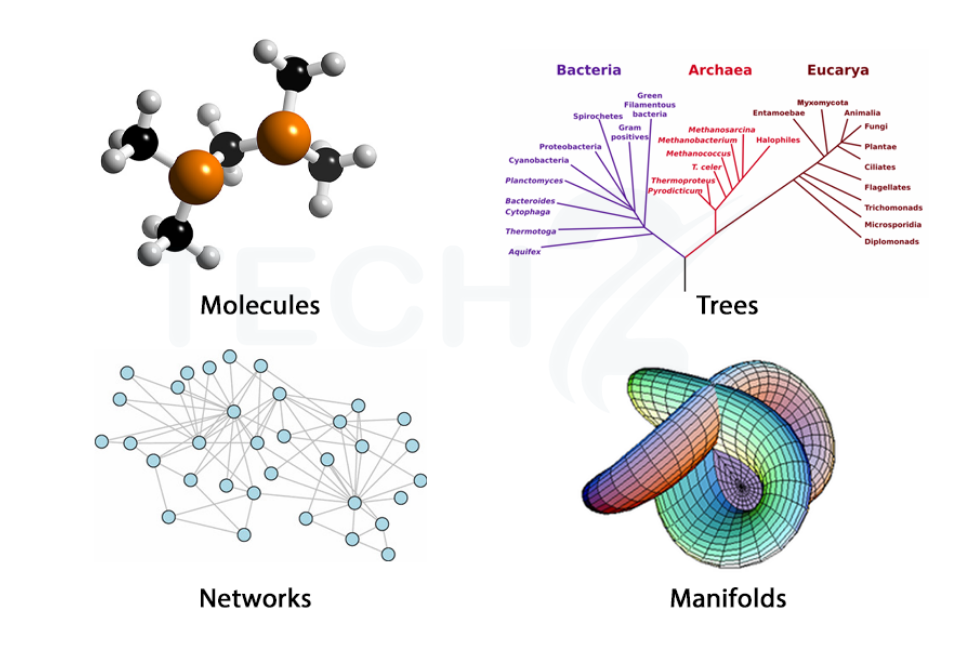
Geometric deep learning (GDL) is a subfield of machine learning that deals with analyzing non-Euclidean data, such as graphs and manifolds. Euclidean data is data that can be represented in a flat space, such as images or text.
Non-Euclidean data, on the other hand, has some kind of inherent structure, such as the connections between nodes in a graph or the curvature of a manifold. This structure is intended to be utilized by GDL approaches to learn more reliable and accurate models.
A like blog – FullStack Deep Learning
These are several basic methods of GDL:
- Graph neural networks (GNNs): A particular kind of neural network made for graphs is the GNN.
It can be used to figure out how nodes in a graph are related to one another, such as how similar two goods are in a system of recommendations or how connected the neurons are in a brain network.
- Manifold learning: These methods are employed to identify the primary low-dimensional order of high-dimensional data sets.
For tasks like clustering and dimensionality reduction, this may be helpful.
- Riemannian geometry: The analysis of curve spaces is known as Riemannian geometry.
Models that are resilient to the curvature of the data can be learned using GDL techniques based on Riemannian geometry.
The topic of GDL is expanding quickly and has many different applications.

The following are some applications for GDL:
- GDL can be used to analyze images and videos using computer vision techniques such as object detection, scene comprehension, and activity recognition.
- GDL can be used to analyze text data for natural language processing tasks like sentiment assessment, automatic translation, and answering questions.
- Medical data analysis using GDL is possible for purposes including diagnosis of diseases, drug discovery, and personalized medicine.
- GDL can be employed to program autonomous systems and operate robots.
- Financial data analysis using GDL is possible for purposes including identifying fraud, risk estimation, and portfolio optimization.
- GDL is an innovative new machine learning strategy that can revolutionize a variety of applications.
- In the years to come, we can anticipate seeing even more fascinating and significant applications of GDL as the field develops.
Additional advantages of employing geometric deep learning include the following:
- It could aid in enhancing the robustness and accuracy of machine learning models.
- It applies to the analysis of data that is difficult to represent in Euclidean space.
- It may be used to discover more intricate connections between the data points.
- It can be used to create scalable and more effective machine-learning algorithms.
A like blog – Deep Residual Learning for image recognition
